• Fitness & Health
• Sport & Exercise Science
• Physical Education
• Strength & Conditioning
• Sports Medicine
• Sport Management
• Dance

What is rank order correlation?

This is an excerpt from Statistics in Kinesiology 5th Edition With Web Resource by Joseph Weir & William Vincent.

Spearman's rank order correlation coefficient is used to determine the relationship between two sets of ordinal data. It is the nonparametric equivalent of Pearson's correlation coefficient. Often data in kinesiology result from experts ranking subjects. For example, a teacher may rank students by skill: 1 (highest skill), 2 (next highest), and so forth on down to the last rank (lowest skill). In recreational sports, ladder and round-robin tournaments may result in a rank order of individuals or teams. Even when data have been collected on a parametric variable, the raw data may be converted to rankings by listing the best score as 1, the next best as 2, and so on.

Ranked data are ordinal and do not meet the criteria for parametric evaluation by Pearson's product moment correlation coefficient. To measure the relationship between rank order scores, we must use Spearman's rank order correlation coefficient (rho, or ρ). The formula for Spearman's rho is

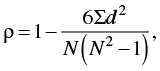(16.04)

where d is the difference between the two ranks for each subject and N is the total number of subjects (i.e., the number of pairs of ranks). The number 6 will always be in the numerator.

The degrees of freedom for ρ are the same as for Pearson's r: df = N_pairs − 2. The significance of ρ is determined by looking up the value for the appropriate degrees of freedom in table A.12 in the appendix.

An Example From Physical Education

We use the tennis example introduced at the beginning of the chapter to demonstrate how to apply Spearman's rho. Recall that the students were ranked from highest (1) to lowest (25) on the serving test. These ranks were then compared with the final placements on the ladder tournament. The results are presented in table 16.6.

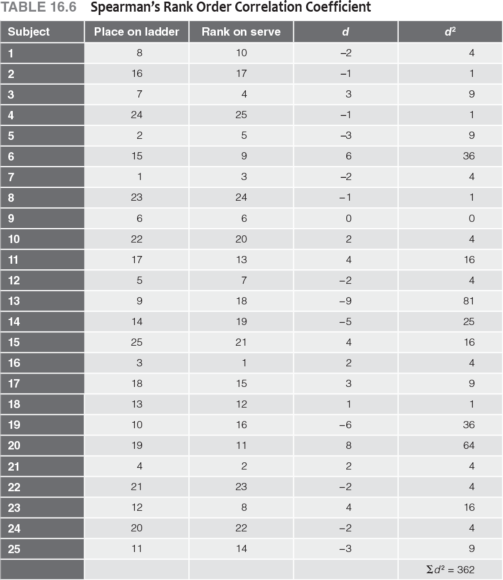
When two scores are tied in ranked data, each is given the mean of the two ranks. The next rank is eliminated to keep N consistent. For example, if two subjects tie for fourth place, each is given a rank of 4.5, and the next subject is ranked 6. In table 16.6, there are no ties because a ladder tournament in tennis does not permit ties; one person must win. The instructor also ranked the students on serving skills without permitting ties.

The difference between each student's rank in the ladder tournament and rank in serving ability was determined, squared, and summed (see table 16.6). The signs of the difference scores are not critical because all signs become positive when the differences are squared. With these values we can calculate ρ by applying equation 16.04:

Table A.12 (in the appendix) indicates that for df = 23, a value of .510 is needed to reach significance at α = .01. The obtained value, .86, is greater than .510, so H₀ is rejected and it is concluded that tennis serving ability and the ability to win tournament games are related at better than the 99% LOC.

Remember, a significant correlation does not prove that being a good server is the cause of winning the game. Many factors are involved in successful tennis ability; serving is just one of them. Other factors related to both serving and winning may cause the relationship.

More Excerpts From Statistics in Kinesiology 5th Edition With Web Resource

---